MA.7.2 函数项级数

一、函数项级数

逐点收敛

• 点态收敛：$x$ 看作常数， $n$ 趋于无穷
• 通项函数列 $\{u_n(x)\}$
• 部分和函数列 $\{v_n(x)\}$

Analysis

$x$ 看成给定的 => 几何级数

Solution

$\sum _{n=1}^{\mathrm{\infty }}=1+x+x^2+\cdots +x^n=\frac{1}{1-x}(|x|<1)$

不一定

$$\text{ 部分和: }{S}_n(x)=1+\sum _{k=1}^n(x^k-x^{k-1})=1+(x^n-1)=x^n$$

限制区间在 $[0,1]$

$$\begin{array}{rl}& \stackrel{n\to \mathrm{\infty }}{⟶}\{\begin{array}{cc}0,& 0<x<1\\ 1& x=1\end{array}\stackrel{\text{ def }}{=}S(x)\underset{x=1\text{ 不连续 }}{\underbrace{\notin C[0,1]}}\end{array}$$

但 $u_n(x)=x^n-x^{n+1}\in C[0,1]$

Solution

$$\begin{array}{rl}& \mathrm{\forall }x\in [0.1]\\ & \sum _{x=0}^{\mathrm{\infty }}{u}_n(x)=\{\begin{array}{ll}0,& x\in {\mathbb{Q}}^c\\ 1,& x\in \mathbb{Q}\end{array}\notin R[0.1]\end{array}$$

$x=r_k$ 代入 $\sum u_n(x)$ 时, 有且只有一项 $=1$ Eg. $x=r_{10}\Rightarrow$ 仅 $u_{10}\left(r_{10}\right)=0$

但 $U_r(x)\in R[0,1]$

Solution

$$\begin{array}{rl}& S_n(x)=2n^{2}x{e}^{-n^2{x}^2}\stackrel{n\to \mathrm{\infty }}{\to }0x\in [0,1]\\ & \therefore {\int }_0^{1}S(x)dx=0\\ & \therefore {\int }_0^{1}2n^{2}x{e}^{-n^3{x}^2}=-{e^{-n^2{x}^2}|}_0^1\\ & =1-e^{-n^2}\\ & \stackrel{n\to \mathrm{\infty }}{\to }1\end{array}$$

结论 $\begin{array}{l}\underset{n\to \mathrm{\infty }}{lim}{\int }_0^{1}2n^{2}x{e}^{-n^2{x}^2}dx\ne {\int }_0^1\left(\underset{n\to \mathrm{\infty }}{lim}2n^{2}x{e}^{-n^{2}x}dx\right)\end{array}$

Solution

$$\begin{array}{rl}{S}_n(x)& =\frac{\sin nx}{\sqrt{x}}\stackrel{n\to \mathrm{\infty }}{\to }0\stackrel{\text{ def }}{=}S(x)\in D(R)\\ S_n^{\prime }(x)& =\sqrt{n}\cos nx\\ nx& =k\pi +\frac{\pi }{2}\Rightarrow x=\frac{k\pi +\frac{\pi }{2}}{n}\end{array}$$

$\because n$ 变化

$\therefore$ 没有 $x$ 使 $nx=\frac{\pi }{2}$

$\therefore$ 当 $n\to \mathrm{\infty }$ 时，无极限

结论

$$\begin{array}{rl}& f_n(x)\stackrel{I}{\to }f(x)\text{ i.e. }\\ \\ & \mathrm{\forall }x\in I,\mathrm{\forall }\epsilon >0,\mathrm{\exists }N\underset{\text{缺乏一致性}}{\underbrace{(\epsilon ,x)}}\in \mathbb{N}，\mathrm{\forall }n>N:\\ & |f_n(x)-f(x)|<\epsilon \end{array}$$

在 $n$ 时刻，同学们和座位的距离小于 $\epsilon$

某个时刻之后都：在教室里

点态收敛：能找到一个时刻大家都到教室里

能否有统一的时刻？只要最后一个人来了

但随着人数增加（$n\to \mathrm{\infty }$）不一定有统一的时间

点态收敛 $\nRightarrow$ 一致收敛

二、一致收敛性

一致收敛

函数级数一致收敛性由 $\{S_n(x)\}$ 一致收敛性定义

若 $f_n(x)\stackrel{I}{\rightrightarrows }f(x)$, 则 $f_n(x)\stackrel{I}{⟶}f(x)$, 反之不然.

定理 (确界极限)

Proof

$⟹$

已知: $\mathrm{\forall }\epsilon >0,\mathrm{\exists }N\in \mathbb{N},\mathrm{\forall }n>N,\mathrm{\forall }x\in I$

有: $|f_n(x)-f(x)|<\epsilon$

$$\begin{array}{rl}& \Rightarrow \underset{a_n}{\underbrace{\underset{x\in I}{sup}|f_n(x)-f(x)|}}⩽\epsilon \\ & \Rightarrow 0⩽a_n\le \epsilon \\ & \Rightarrow \underset{n\to \mathrm{\infty }}{lim}{a}_n=0\end{array}$$

i.e. ${\displaystyle \underset{n\to \mathrm{\infty }}{lim}\underset{x\in I}{sup}|f_n(x)-f(x)|⩽\epsilon }$

$⟸$

已知: $\mathrm{\forall }\epsilon >0,\mathrm{\exists }N\in \mathbb{N},\mathrm{\forall }n>N$

$$\underset{x\in I}{sup}|f_n(x)-f(x)|<\epsilon$$

故 $\mathrm{\forall }\epsilon \in I$ 有

$$|f_n(x)-f(x)|⩽\underset{x\in I}{sup}|f_n(x)-f(x)|<\epsilon$$

Solution

$$\begin{array}{rl}& f_n(x)=\frac{1}{x+n}\stackrel{[0,1]}{⟶}0,\mathrm{又}\\ & |f_n(x)-0|=\frac{1}{x+n}\\ & \text{ 故 }\underset{x\in [0,1]}{sup}\frac{1}{x+n}=\frac{1}{n}\stackrel{n\to \mathrm{\infty }}{\to }0\\ & ⟹f_n(x)\stackrel{[0,1]}{\rightrightarrows }0\end{array}$$

Proof

由前已求 $S_n(x)=x^n\to \{\begin{array}{ll}0,& 0\le x<1\\ 1,& x=1\end{array}\stackrel{\text{det}}{=}S(x)$

故 $|S_n(x)-S(x)|=\{\begin{array}{ll}{x}^n,& 0\le x<1\\ 0,& x=1\end{array}$

可画图

$$\Rightarrow \underset{x\in [0,1]}{sup}|S_n(x)-S(x)|=1\ne 0$$

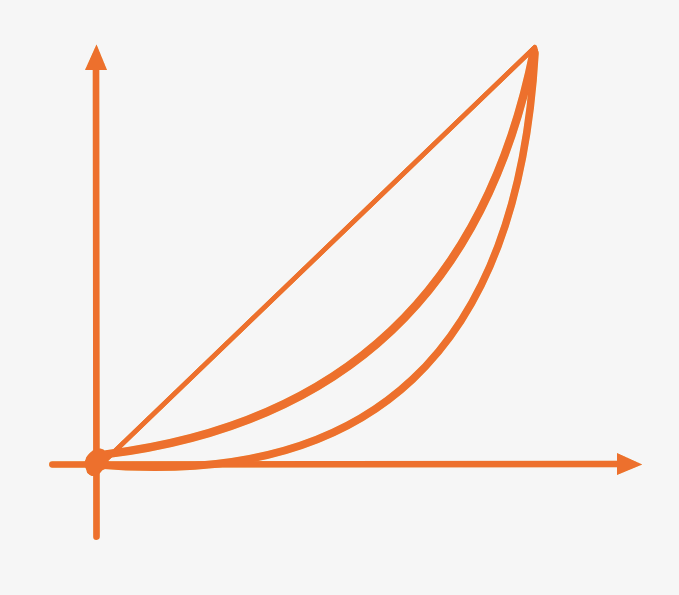
$\therefore$ 原函数在 $[0.1]$ 上非一致收敛

定理(Cauchy 一致收敛准则)

Proof

$⟹$

设 $f_n(x)\stackrel{I}{\rightrightarrows }f(x)$, 则 $\mathrm{\forall }\epsilon >0,\mathrm{\exists }N\in \mathbb{N},\mathrm{\forall }n>N,\mathrm{\forall }x\in I$

$$|f_n(x)-f(x)|<\frac{\epsilon }{2}$$

$\mathrm{\forall }p\in \mathbb{N},n+p>N$ 故 $|f_{n+p}(x)-f(x)|<\frac{\epsilon }{2}$

$$\Rightarrow |f_{n+p}(x)-f_n(x)|\le |f_{n+p}(x)-f(x)|+|f(x)-f_n(x)|<\frac{\epsilon }{2}+\frac{\epsilon }{2}=\epsilon$$

---

$⟸$

已知: $\mathrm{\forall }\epsilon >0,\mathrm{\exists }N\in \mathbb{N},\mathrm{\forall }n>N,\mathrm{\forall }p\in \mathbb{N},\mathrm{\forall }x\in I$

$$|f_{n+p}(x)-f_n(x)|<\epsilon$$

$\mathrm{\forall }$ 固定的 $x\in I$ ，由数列 Cauchy: $f_n(x)$ 收敛
可设 $\underset{n\to \mathrm{\infty }}{lim}{f}_n(x)\stackrel{\mathrm{def}}{=}f(x)$

此时令 $p\to \mathrm{\infty }:|f(x)-f_n(x)|<\epsilon$
即: $f(x)\stackrel{I}{\rightrightarrows }f(x)$

$$\begin{array}{rl}|S_{n+p}(x)-S_n(x)|& =|\sum _{k=n+1}^{n+p}{u}_k(x)|\\ & <\epsilon \end{array}$$

Solution

由 Cauchy: $\mathrm{\forall }\epsilon >0,\mathrm{\exists }N\in \mathbb{N},\mathrm{\forall }n>N,\mathrm{\forall }p\in \mathbb{N},\mathrm{\forall }x\in (a,+\mathrm{\infty })$ :

$$\begin{array}{rl}& |\sum _{k=n+1}^{n+p}{u}_k(x)|<\frac{\epsilon }{2}<\epsilon \\ \Rightarrow & |\sum _{k=n+1}^{n+p}{u}_k(a)|=\underset{x\to a^{+}}{lim}|\sum _{k=n+1}^{n+p}{u}_k(x)|⩽\frac{\epsilon }{2}<\epsilon \end{array}$$

由数项级数 $u_n(a)$ 收敛的Cauchy
知: $\sum _{n=1}^{\mathrm{\infty }}{u}_n(a)$ 收敛且 $a\in [a,+\mathrm{\infty })\text{ i.e. }\mathrm{\forall }a\in [a,+\mathrm{\infty })$

$$|\sum _{n=1}^{\mathrm{\infty }}{u}_n(x)|<\epsilon$$

即: $\sum _{n=1}^{\mathrm{\infty }}{u}_n(x)$ 在 $[a,+\mathrm{\infty })$ U.C.

取 $p\in (1,x)\dots$ 使 $l=0$

$$\underset{n\to \mathrm{\infty }}{lim}{n}^2\frac{\ln n}{n^x}=\underset{x-p\text{ 为正数 }}{\underbrace{\underset{n\to \mathrm{\infty }}{lim}\frac{\ln n}{n^{x-p}}}}=0(l=0)$$

由p-判: $\sum _{n=1}^{\mathrm{\infty }}\frac{\ln n}{n^x}$ 收敛

由于 $\frac{\ln n}{n^x}\in C[1,+\mathrm{\infty })$ 且当 $x=1$ 时
$\sum _{n=1}^{\mathrm{\infty }}\frac{\ln n}{n}$, 发散 $(\frac{\ln n}{n}>\frac{1}{n}(n⩾3))$

由Co. $\sum _{n=2}^{\mathrm{\infty }}\frac{\ln n}{n^x}$ 在 $(1,+\mathrm{\infty })$ 非U.C

Analysis

$x=0$ 发散

Weierstrass 判别法

优(控制)级数: $\sum _{n=1}^{\mathrm{\infty }}{a}_n$ $\dots a_n\mathrm{来}\mathrm{控}\mathrm{制}{u}_n$
寻找优级数: 常放大

Analysis

Cauchy 一致收敛 + 放缩寻找优级数

Proof

由于 $\sum _{n=1}^{\mathrm{\infty }}{a}_n$ 收敛， $\mathrm{\forall }\epsilon >0，\mathrm{\exists }N\in \mathbb{N},\mathrm{\forall }n>N，\mathrm{\forall }p\in \mathbb{N}$, 有

$$|\sum _{k=n+1}^{n+p}{u}_k(x)|⩽\sum _{k=n+1}^{n+p}|u_k(x)|⩽\sum _{k=n+1}^{n+p}{a}_k<\epsilon$$

Proof

$$\begin{array}{rl}& \frac{\cos nx}{n^{\alpha }}⩽\frac{1}{n^{\alpha }}\text{ 且 }\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^{\alpha }}\text{ 收敛 }(x\in \mathbb{R})\\ & \text{ 由W-判: }\sum _{n=1}^{\mathrm{\infty }}\frac{\cos nx}{n^{\alpha }}\text{ 在 }\mathbb{R}\text{ 上U.C. }\end{array}$$

定理(A-D判别法)

Analysis

$$|\sum _{k=n+1}^{n+p}{U}_k(x)V_k(x)|⩽?(|V_{n+1}(x)|+2|U_{n+p}(x)|)$$

其中 $|A_k(x)|=\underset{\text{ 一致收敛, 可出 }\epsilon }{\underbrace{|\sum _{i=1}^k{U}_{n+i}(x)|⩽?}}=\frac{\epsilon }{3M}$

Proof (Abel)

由 $\sum _{n=1}^{\mathrm{\infty }}{u}_n(x)$ 在 E上u.c. $\mathrm{\forall }\epsilon >0,\mathrm{\exists }N\in N$,
$\mathrm{\forall }n>N,\mathrm{\forall }k\in \mathbb{N},\mathrm{\forall }x\in E$, 有

$$|A_k(x)|=|\sum _{i=n+1}^{n+k}{u}_i(x)|\le \frac{\epsilon }{3M}$$

从而 $\mathrm{\forall }p\in \mathbb{N}$, 由 Abel Lemma:

$$|\sum _{k=n+1}^{n+p}{u}_k(x)V_k(x)|=\frac{\epsilon }{3M}(|V_{n+1}(x)|+2|U_{n+p}(x)|)⩽\frac{\epsilon }{3M}\cdot 3M=\epsilon$$

Proof

令 $V_n(x)=\frac{1}{n}$ ，则 $V_n(x)\stackrel{(\delta ,\pi )}{⟹}0$ ，且 $\{V_n(x)\}$ 关于n单调
又

$$\begin{array}{rl}{S}_n(x)& =\sum _{k=1}^n\sin kx=\frac{1}{2\sin \frac{x}{2}}\sum _{k=1}^{n}2\sin kx\sin \frac{x}{2}\\ & =\frac{1}{2\sin \frac{x}{2}}\sum _{k=1}^n(\cos (k-\frac{1}{2})x-\cos (k+\frac{1}{2})x)\\ & =\frac{\cos \frac{x}{2}-\cos (n+\frac{1}{2})x}{2\sin \frac{x}{2}}\end{array}$$

故 $\mathrm{\forall }x\in [\delta ,\pi ]|\sin (x)|\le \frac{1}{2\sin \frac{x}{2}}\le \frac{1}{2\sin \frac{\delta }{2}}\frac{\text{ 一致有界 }}{\text{ D. 判 }}$ U.C.

Solution

$$\begin{array}{rl}& \text{ 令 }{V}_n(x)=\frac{1}{n^x}，U_n(x)=a_n\text{ 则 }\mathrm{\forall }x\in [0,+\mathrm{\infty })\\ & \{u_n(x)\}\text{ 关于n单减 且 }0⩽\frac{1}{n^x}\le 1\text{ 即 }\{u_n(x)\}\text{ 一致有界 }\\ & \text{ 又 }\sum _{n=1}^{\mathrm{\infty }}{a}_n\text{ 收敛，通项不含 }x\Rightarrow \text{ 一致收敛 }\end{array}$$

由 Abel Lemma: 原级数U.C.

三、一致收敛级数的性质

定理 (连续性)

Tips

=> 三分$\epsilon$

Analysis

$\mathrm{\forall }$ 固定 $x_0\in I$ ，令 $S_n(x)=\sum _{k=1}^n{U}_k(x)$

$$\text{ 即 }{S}_n(x)\stackrel{I}{\rightrightarrows }S(x)$$

连续的定义

$$\begin{array}{rl}& |S(x)-S\left(x_0\right)|<\epsilon \\ & \text{ 差分 (三分) }\\ & |S(x)-S\left(x_0\right)|⩽|S_N(x)-S(x)|+|S_N(x)-S\left(x_0\right)|\\ & \le |S_N(x)-S(x)|+\underset{u_n(x)\in C⟹S_N\in C\stackrel{x\to x_0}{\Rightarrow }\frac{\epsilon }{3}}{\underbrace{S_N(x)-S_N\left(x_0\right)\mid }}+|S_N\left(x_0\right)-S\left(x_0\right)|\\ & \end{array}$$

Proof

由条件 $S_n(x)\stackrel{I}{⟶}S(x)\mathrm{\forall }\epsilon >0,\mathrm{\exists }N\in \mathbb{N},\mathrm{\forall }x\in I$ 有

$$|S_N(x)-S(x)|<\frac{\epsilon }{3}|S_N(x)-S\left(x_0\right)|<\frac{\epsilon }{3}$$

又 $S_N(x)$ 在 $x_0$ 连续，对上述 $\epsilon >0，\mathrm{\exists }\delta (\epsilon )>0，\mathrm{\forall }|x-x_0|<\delta$, 有

$$|S_N(x)-S_N\left(x_0\right)|<\frac{\epsilon }{3}$$

从而 $|S(x)-S\left(x_0\right)|<\dots <\frac{\epsilon }{3}+\frac{\epsilon }{3}+\frac{\epsilon }{3}=\epsilon$

特别地，若 $I$ 为开区间，则可以找到一个闭子区间 $[\alpha ,$ $\beta ]$ 使得在该区间上一致收敛，即：一致收敛可减弱为内闭一致收敛

弱形式: 内闭一致收敛

• 对于闭区间：一致收敛 <=> 内闭一致
• 对于开区间：一致收敛 <== 内闭一致

反例：

Proof

已知 $S_n(x)=x^n\to 00\le x<1$
$\mathrm{\forall }[a,b]<[0,1)$ 则 $b<1$, 从而

$$\underset{x\in [a,b]}{sup}|S_n(x)-0|=\underset{x\in [a,b]}{sup}{x}^n=b^n\stackrel{n\to \mathrm{\infty }}{⟶}0$$

故 $S_n(x)\stackrel{[a,b]}{\rightrightarrows }0,(b$ 固定) $\Rightarrow$ 内闭U.C.
而 $S_n(x)$ 在 $[0,1)$ 上确界为 $1\Rightarrow$ 非U.C.

Proof

(2) $\mathrm{\forall }[a,b]c(0,+\mathrm{\infty })$ 则 $a>0$ ， 当 $x\in [a,b]$ 时.

$$0<u_n(x)=n{e}^{-nx}=\frac{n}{e^{nx}}⩽\frac{n}{e^{na}}$$

且 $\sum _{n=1}^{\mathrm{\infty }}\frac{n}{e^{na}}$ 收敛（根值: $\underset{n\to \mathrm{\infty }}{lim}\frac{\sqrt[n]{n}}{e^a}=\frac{1}{e^a}<1$ )
$\stackrel{w-\text{ 判 }}{\Rightarrow }\sum n{e}^{-nx}$ 在 $[a,b]$ 上 U.C. =>即 $(0,+\mathrm{\infty })$ 内闭U.C.
$\stackrel{\text{ 连续性 }}{\Rightarrow }S(x)\in C(0,+\mathrm{\infty })$

取1时发散
(1) $u_n(x)=\frac{1}{n^x}\in C(1,\mathrm{\infty })$
(2) $\mathrm{\forall }[a,b]\subset [1,+\mathrm{\infty })$ 则 $a>1$ 且 $\mathrm{\forall }x\in [a,b]$ $0<u_n(x)=\frac{1}{n^x}\le \frac{1}{n^a}$, 且 $\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^a}$ 收敛
$\stackrel{W-\mathrm{判}}{\to }$ $\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^x}$ 在 $[a,b]$ 上U.C. , 即在 $(1,+\mathrm{\infty })$ 内闭U.C.
$\stackrel{\text{ 连续 }}{\to }S(x)\in C(1,+\mathrm{\infty })$

定理 (逐项可积性)

• 和的积分=积分的和（无限）

Analysis

$$\text{ 令 }{S}_n(x)=\sum _{k=1}^n(x)\text{ 则 }{S}_n(x)=\sum _{k=1}^n{u}_k(x)\text{. 则 }{S}_n(x)\stackrel{[a,b]}{⟹}S(x)$$

即证 $\underset{x\to 0}{lim}{\int }_a^b{S}_n(x)dx={\int }_a^{h}S(x)dx$

Proof
由条件 $\mathrm{\forall }\epsilon >0,\mathrm{\exists }N\in \mathbb{N},\mathrm{\forall }n>N,\mathrm{\forall }x\in [a,b]$, 有

$$|S_n(x)\cdot S(x)|<\frac{\epsilon }{b-a}$$

$\Rightarrow$

$$\begin{array}{rl}\mid {\int }_a^b{S}_n(x)dx-\underset{S_n(x)\in c}{\underbrace{{\int }_a^{b}S(x)dx\mid }}& =\left|{\int }_a^b(S_n(x)-S(x))dx\right|\\ & ={\int }_a^b|S_n(x)-S(x)|dx\\ & <\frac{\epsilon }{b-a}\cdot (b-a)\\ & =\epsilon \end{array}$$

由于 ${\int }_a^h{S}_n(x)dx={\int }_a^b\underset{\mathrm{有}\mathrm{限}\mathrm{项}}{\underbrace{\sum _{k=1}^n{u}_k(x)}}dx\stackrel{\text{ 积分线性性 }}{=}\sum _{k=1}^n{\int }_a^b{u}_k(x)dx$
故 $\underset{n\to \mathrm{\infty }}{lim}{\int }_a^b{s}_n(x)dx=\sum _{k=1}^{\mathrm{\infty }}{\int }_a^b{u}_n(x)dx$

注 据连续性定理: $S\in C[a,b]$, 从而 $S\in R[a,b]$

注 条件 “ $u_n\in C[a,b]$ ” 可减弱为 “ $u_n\in R[a,b]$ ”
（证明较难）

Analysis

W-判：发散

Solution

$\mathrm{\angle }15:$
(1) $\frac{\cos nx}{n^2}\in C[0,\pi ]$
(2) $\mathrm{\forall }x\in [0,\pi ]，\frac{|\cos nx|}{n^2}\le \frac{1}{n^2}$ 且 $\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2}$ 收敛
$\stackrel{w-\mathrm{判}}{\to }\sum _{n=1}^{\mathrm{\infty }}\frac{\cos nx}{n^2}$ 在 $[0,\pi ]$ U.C.
故

$$\begin{array}{rl}{\int }_0^{\pi }f(x)dx& ={\int }_0^{\pi }\sum _{n=1}^{\mathrm{\infty }}\frac{\cos nx}{n^2}dx\\ & =\sum _{n=1}^{\mathrm{\infty }}{\int }_0^{\pi }\frac{\cos nx}{n^2}dx\\ & =\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2}{\int }_0^{\pi }\cos nxdx\\ & ={\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2}\left(\frac{\sin nx}{n}\right)|}_0^{\pi }\\ & =\sum _{n=1}^{\mathrm{\infty }}0\\ & =0\end{array}$$

定理 (逐项可微性)

• 先求和再求导=先求导再求和（无限）

Analysis

$$S_{n^{\prime }}(x)={(\sum _{k=1}^n{u}_k(x))}^{\prime }=\sum _{k=1}^n{u}_k^{\prime }(x)$$

条件(3)变为:

$$\{S_n^{\prime }(x)\}\text{ 在 }[a,b]\mathrm{上}U.C.$$

归一法: 证明和函数唯一
设 $S_n^{\prime }(x)\stackrel{[a,b]}{\rightrightarrows }f(x)$ (必有和函数) $(=\sum _{n=1}^{\mathrm{\infty }}{u}_n^{\prime }(x))$
下证: $f(x)=S^{\prime }(x)$ 即可

Proof

$\mathrm{\forall }$ 固定 $x\in [a,b],{}^{\prime }{u}_n^{\prime }(t)\in c[a,x]\dots$ (2)
且 $\sum _{n=1}^{\mathrm{\infty }}{u}_n^{\prime }(t)$ 在 $[a,x]$ U.c.... (s)
由可积性，两边积分

$$\begin{array}{rl}{\int }_a^{x}f(t)dt& =\sum _{n=1}^{\mathrm{\infty }}{\int }_a^x{u}_n^{\prime }(t)=\sum _{n=1}^{\mathrm{\infty }}[u_n(x)-u_n(a)]\\ & =S(x)-S(a)\dots (1)\end{array}$$

由于f连续: 两边求导:

$$f(x)=S^{\prime }(x)$$

Solution
(1) $\mathrm{\forall }x\in (1,+\mathrm{\infty })\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^x}$ 收敛 $(=\zeta (x))$
(2) ${\left(\frac{1}{n^x}\right)}^{\prime }=\frac{\ln n}{n^x}\in c(1,+\mathrm{\infty })$
(3)
弱形式：$\mathrm{\forall }x\in [a,b]$ 有

$$\left|\frac{\ln n}{n^x}\right|=\frac{\ln n}{n^x}<\frac{\ln n}{n^a}$$

(p-判) 取 $p\in (1,a)$, 则

$$\underset{n\to \mathrm{\infty }}{lim}{n}^p\frac{\ln n}{n^a}=\underset{n\to \mathrm{\infty }}{lim}\frac{\ln n}{n^{a-p}}=0$$

由p-判: $\sum _{n=1}^{\mathrm{\infty }}\frac{\ln n}{n^a}$ 收敛
由W-判: $\sum _{n=1}^{\mathrm{\infty }}\frac{\ln n}{n^x}$ 在 $[a,b]\mathrm{上}U.C.$ 。

即在 $(1,+\mathrm{\infty })$ 内闭 U.C.
从而 $S^{\prime }(x)\in C(1,+\mathrm{\infty })$ 且

$$S^{\prime }(x)=-\sum _{n=1}^{\mathrm{\infty }}\frac{\ln n}{n^x}(x\in (1,+\mathrm{\infty }))$$

命题 (无穷远处连续性)